

I took 3 sets of pictures for mosaics and 2 pictures for image rectification. For the mosaic pictures it was VERY important to rotate about the cameras lens and not my own head. If this was not done the homographies would have been off.











In order to create the mosaic'd images, we need to compute a homography matrix, so we can perform the operation below.
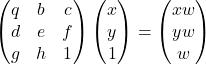
On each image we will set 4 corresponding points, typically corners of windows, or buildings. This way we know both coordinates of the corresponding image. If we rearrange our equation to the form Ax = b, where x is a vector of all unknowns, we can use least squares to solve for all the values in the homography matrix.
So again if we define a set of four or more corresponding points between two images (or just one image and some set of points), we can warp any which way we please. Once we have the homography matrix, you can matrix multiply every index of an image, and take the pixel values from every corresponding point.
This step leverages the warping function to take some object and make it a rectangle. It can be really helpful if you have an object that might already be a rectangle, but the angle of the image makes it seem almost like a trapezoid. We can plot points on the corner of whatever rectangle we have and morph it to some linear combination of the 2d cartesian basis vectors.






Finally now we have all the peices in place to create a mosaic. Firstly I had 3 images, a middle and left/right or top/bottom. Then I found corresponding points from the side image to the middle image, computed a homography, then warped each image to the middle. Finally I stiched it all together making sure to properly align the corresponding points. I also computed a mask to help blend all the images together.



These turned out really well, particularly the blending was much smoother than I would have ever thought. In my code I had some problem keeping the output images of a certain size so I over compensated a bit.
Above is a cool way to make panoramics, but theres one huge problem. You have to load your image up into some software, pick the correspondence points, then I can sititch them together. Its cumbersome, why not do this first part automatically?
Thankfully our professor has provided code that automatically finds points of interest, along with computing a heat map for how 'interesting' each pixel in the image is. Below is all points the detector chose on my two images.
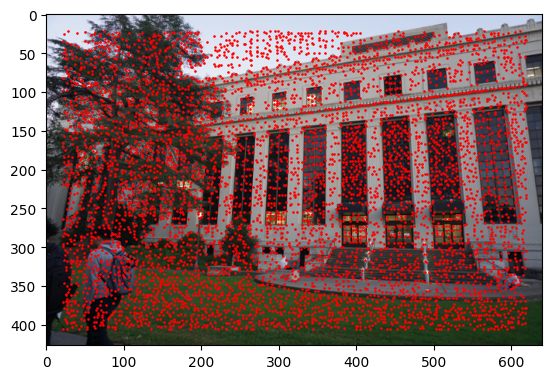
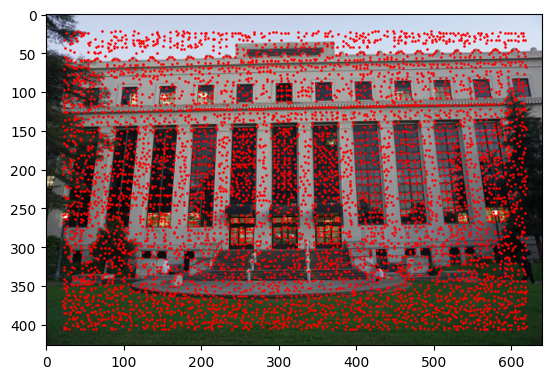
Now that we have all these points, to speed some things up we want to surpress "bad points" and keep prominent ones all while keeping a nice spread of points over the image. I implemented Adaptive Non-Maximal Suppression, which does just that. Below are the remaning points in the image.
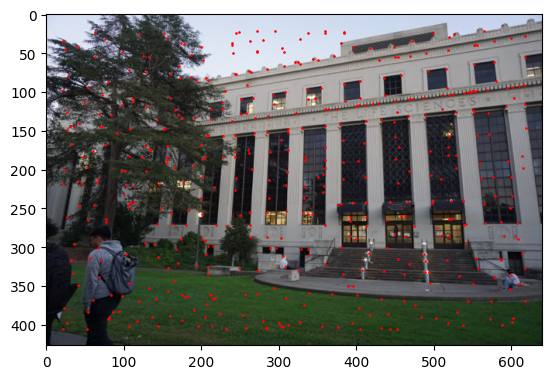
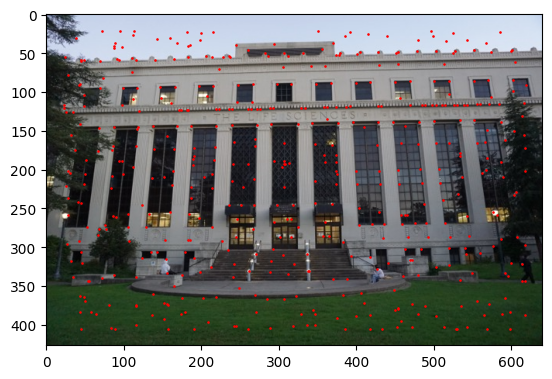
With these points we create features to do K-nearest neighbors, for us the features will be a 40x40 pixel patch around our point, which we will rescale to 8x8. Below are some samples of patches from the middle image. To match these fetures we a K-nearest neighbors, if the two nearest neighbors are not that great of a choice, we throw the paring out alltogether.

Now given these matching points, to further filter out bad matches, we use RANSAC to test out many differnent combinations of 4 pairings to calculate a homography. Then we can calculate the effect of that homography on the rest of the points, then find out how good each pairing is, keeping track of how many points it transformed correctly. We save which homography transforms the most points correctly.
Now all the pieces are together to achieve our dream of creating a mosaic from 3 images. Below are a side by side of the manual point picking vs the automatic corner detection.






The automatic images are much better aligned than the hand ones which I am very happy about. I enjoyed reading the research paper to remake their results, even if the ANMS paragraph took several read overs to comprehend. My favorite thing I learned was about how changing where the camera is located in space can and will mess up the mosaicing since geometries change, even if just slightly, whent he perspective changes.